complex(): complex number from a real and an imaginary component

x=complex(4,3)
print(type(x)) # <class 'complex'>
print(x)       # (4+3j)

Real and Imaginary parts

x=complex(4,3)
print(x.real)       # 4.0
print(x.imag)       # 3.0
print(type(x.imag)) # <class 'float'>
print(type(x.real)) # <class 'float'>

x=complex('4+3j')
print(type(x)) # <class 'complex'>

x=complex('4+3j',4)

Understanding the Complex Number Object in Python

In Python, complex numbers are represented using the complex class. These numbers consist of a real and an imaginary part.

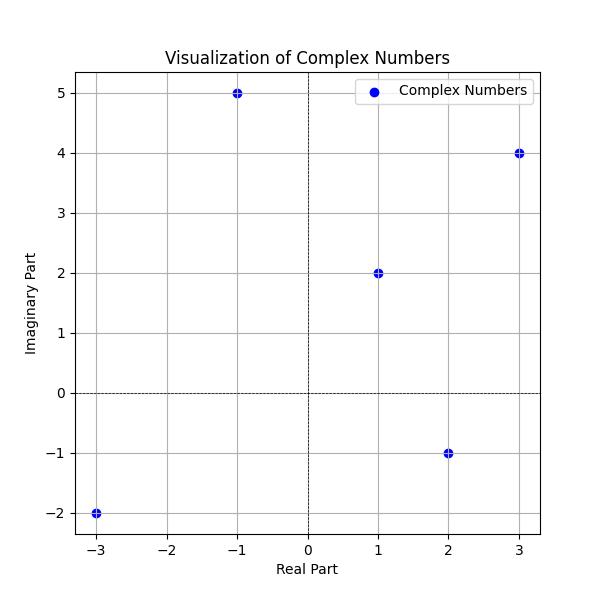
Example 1: Visualizing Complex Numbers

To better understand complex numbers, we can visualize them on a 2D plane. The real part lies on the x-axis, and the imaginary part lies on the y-axis. Here's how we can plot complex numbers using Matplotlib:

import matplotlib.pyplot as plt

# List of complex numbers
complex_numbers = [3 + 4j, 1 + 2j, -1 + 5j, -3 - 2j, 2 - 1j]

# Separate real and imaginary parts
real_parts = [z.real for z in complex_numbers]
imag_parts = [z.imag for z in complex_numbers]

# Plotting
plt.figure(figsize=(6, 6))
plt.axhline(0, color='black', linewidth=0.5, linestyle='--')
plt.axvline(0, color='black', linewidth=0.5, linestyle='--')
plt.scatter(real_parts, imag_parts, color='blue', label='Complex Numbers')
plt.title('Visualization of Complex Numbers')
plt.xlabel('Real Part')
plt.ylabel('Imaginary Part')
plt.grid(True)
plt.legend()
plt.show()

Output:

Example 2: Discarding Complex Numbers Conditionally

We can filter complex numbers based on conditions. For instance, let’s discard numbers with a magnitude greater than a threshold:

import math

complex_numbers = [3 + 4j, 1 + 2j, -1 + 5j, -3 - 2j, 2 - 1j]
threshold = 5

# Filter complex numbers with magnitude <= threshold
filtered_numbers = [z for z in complex_numbers if abs(z) <= threshold]

print("Filtered Complex Numbers:", filtered_numbers)

Output:

Filtered Complex Numbers: [(3+4j), (1+2j), (-3-2j), (2-1j)]

Example 3: Rotating Complex Numbers

Rotation is a common operation for complex numbers, useful in physics and engineering. Rotating a complex number involves multiplying it by another complex number representing the rotation angle:

import cmath
import math

z = 3 + 4j
angle = math.radians(45)  # Rotation by 45 degrees

# Rotation
rotated_z = z * cmath.exp(1j * angle)

print("Original Complex Number:", z)
print("Rotated Complex Number:", rotated_z)

Output:

Original Complex Number: (3+4j)
Rotated Complex Number: (-0.7071067811865475+4.949747468305834j)

Applications of Complex Numbers in Python

• Signal Processing: Complex numbers are heavily used in Fourier transforms and digital signal processing (DSP).
• Electrical Engineering: Useful for representing AC circuits and impedance calculations.
• Physics: Applications include quantum mechanics and wave equations.
• Graphics and Animation: Complex numbers simplify rotation and scaling transformations in 2D graphics.

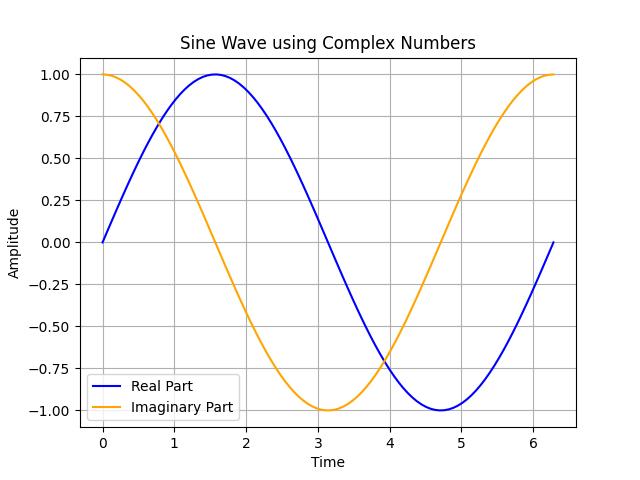
Code Example: Signal Processing Using Complex Numbers

Here’s an example of how we can generate and visualize a simple sine wave using complex numbers:

import numpy as np
import matplotlib.pyplot as plt

# Generate a sine wave using complex numbers
t = np.linspace(0, 2 * np.pi, 100)
sine_wave = np.sin(t) + 1j * np.cos(t)

# Plot real and imaginary parts
plt.plot(t, sine_wave.real, label='Real Part', color='blue')
plt.plot(t, sine_wave.imag, label='Imaginary Part', color='orange')
plt.title('Sine Wave using Complex Numbers')
plt.xlabel('Time')
plt.ylabel('Amplitude')
plt.legend()
plt.grid(True)
plt.show()

Output:

Subhendu Mohapatra

Author

🎥 Join me live on YouTube

Passionate about coding and teaching, I publish practical tutorials on PHP, Python, JavaScript, SQL, and web development. My goal is to make learning simple, engaging, and project‑oriented with real examples and source code.

← Subscribe to our YouTube Channel here