asinh() math function to get inverse hyperbolic sin of x input number in radian in Python

asinh(x) returns inverse hyperbolic sin of x , the input number x is in radian.

import math
print(math.asinh(1))       # 0.8813735870195429
print(math.asinh(1.5))     # 1.1947632172871094
print(math.asinh(5))       # 2.3124383412727525

Note that all the inputs are in radian.
With negative input numbers

import math
print(math.asinh(-1))    #  -0.8813735870195429
print(math.asinh(-8.1))  #  -2.788800040920179

Inputs in degree

We can convert radian value to degree and use the same

import math
in_degree = 60
in_redian = math.radians(in_degree)
print(math.asinh(in_redian)) # 0.9143566553928859

Output

0.9143566553928859

1 radian = 57.2957914331 degree
1 degree = 0.0174533 radian

Drawing graph of asinh()

We will use Matplotlib to generate graph of asinh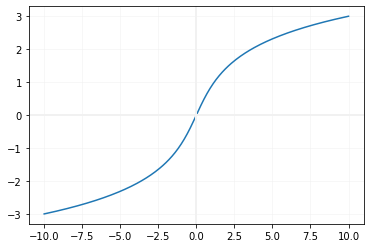 $asinh graph$

import matplotlib.pyplot as plt
x=[]
y=[]
i=-10
while (i<=10):
    x.append(i)
    y.append(math.asinh(i))
    i=i+0.1
plt.plot(x,y)
plt.axvline(x=0.00,linewidth=2, color='#f1f1f1')
plt.axhline(y=0.00,linewidth=2, color='#f1f1f1')
plt.grid(linestyle='-',
    linewidth=0.5,color='#f1f1f1')
plt.show()

Example 1: Handling Negative Inputs

import math
print(math.asinh(-2))  # Output: -1.4436354751788103

Example 2: Using cmath for Complex Numbers

import cmath
z = complex(2, 3)
print(cmath.asinh(z))  # Handles complex input

Output

(1.9686379257930964+0.9646585044076028j)

Example 3: Hyperbolic Calculations in Engineering

import math
x = 1.5
result = math.asinh(x)
print(result)  # Output: 1.1947632172871094

Math Functions copysign() Python- Tutorials

Subhendu Mohapatra

Author

🎥 Join me live on YouTube

Passionate about coding and teaching, I publish practical tutorials on PHP, Python, JavaScript, SQL, and web development. My goal is to make learning simple, engaging, and project‑oriented with real examples and source code.

Subscribe to our YouTube Channel here