sinh()

import math
print(math.sinh(-1))       # -1.1752011936438014
print(math.sinh(-1.5))     # -2.1292794550948173
print(math.sinh(-5))       # -74.20321057778875
print(math.sinh(0))        # 0.0
print(math.sinh(1))        # 1.1752011936438014
print(math.sinh(1.5))      # 2.1292794550948173
print(math.sinh(5))        # 74.20321057778875

Inputs in degree

import math
in_degree = 60
in_redian = math.radians(in_degree)
print(math.sinh(in_redian)) # 1.2493670505239751

Drawing graph of sinh()

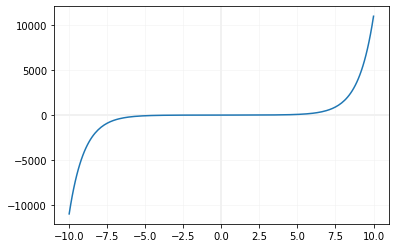
import matplotlib.pyplot as plt
x=[]
y=[]
i=-10
while (i<=10):
    x.append(i)
    y.append(math.sinh(i))
    i=i+0.1
plt.axvline(x=0.00,linewidth=2, color='#f1f1f1')
plt.axhline(y=0.00,linewidth=2, color='#f1f1f1')
plt.plot(x,y)
plt.grid(linestyle='-',
    linewidth=0.5,color='#f1f1f1')
plt.show()

Example 1: Symmetry of sinh()

import math
x = 2
print(math.sinh(x))   # Output: 3.626860407847019
print(math.sinh(-x))  # Output: -3.626860407847019 (symmetric)

Example 2: Calculating sinh() for Small Angles

import math
angle = 0.1  # Small angle in radians
print(math.sinh(angle))  # Output: 0.10016675001984403

Example 3: Calculating sinh() for Large Values

import math
large_value = 10
print(math.sinh(large_value))  # Output: 11013.232874703393

Example 4: Using sinh() in a Mathematical Formula

import math
x = 1.5
y = 2.0
result = 2 * math.sinh(x) + 3 * math.sinh(y)
print(result)  # Output: 15.13914013373069

Example 5: Comparing sinh() with Other Hyperbolic Functions

import math
x = 2.0
sinh_val = math.sinh(x)
cosh_val = math.cosh(x)
tanh_val = math.tanh(x)
print(f"sinh: {sinh_val}, cosh: {cosh_val}, tanh: {tanh_val}")

sinh: 3.6268604078470186, cosh: 3.7621956910836314, tanh: 0.9640275800758169

Subhendu Mohapatra

Author

🎥 Join me live on YouTube

Passionate about coding and teaching, I publish practical tutorials on PHP, Python, JavaScript, SQL, and web development. My goal is to make learning simple, engaging, and project‑oriented with real examples and source code.

← Subscribe to our YouTube Channel here